[이론공부] 검색 구조 => 선형검색과 이진검색. 그리고 BigO
1. 선형검색 (Linear Search)

가장 기초적인 검색방법이라 볼 수 있다.
배열의 index 상자들을 0부터 하나하나 열어보면서 내가 찾고자 하는 '7' 이라는 데이터가 있는지를 확인하는 것이다.
이 경우 최악의 시나리오는 배열의 가장 마지막에 '7'의 데이터가 있거나 혹은 이 배열 안엔 '7' 이라는 데이터가 없을 때.
이처럼 배열, 그리고 input 사이즈의 크기가 N이라고 했을 때 선형검색은 N번 만큼의 과정, 스텝이 필요로 해지게 된다.
이를 BigO 라는 표현으로 쓸 때 선형검색의 시간복잡도 = O(N) 이라고 표현한다.
2. 이진검색 (Binary Search)
이진검색의 기본 조건은 정렬(Sorting)이다.
정렬되어있지 않은 데이터구조, 배열에는 이진검색을 사용할 수 없다.
따라서 이진검색이 사용되는 배열에는 데이터를 추가하거나 삭제할 때마다 정렬이 이루어진다.
그렇기 때문에 아무런 작업이 이루어지지 않는 배열에 데이터를 추가할 때보다 이진검색이 적용된 배열에 데이터를 추가할 때 시간복잡도(시간) 이 더 걸린다.
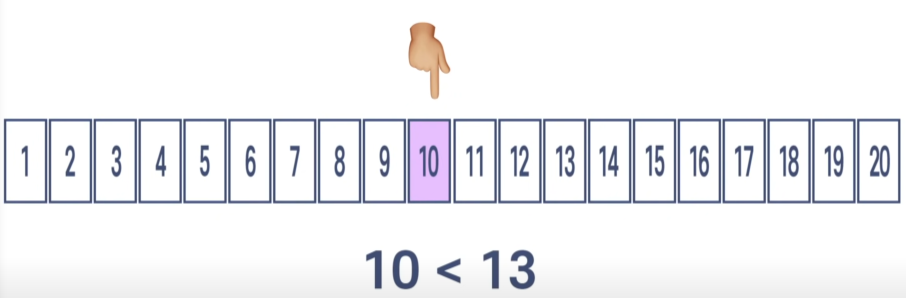



하지만 이진검색의 장점은 검색의 효율성이다.
위 그림에서와 같이 13이라는 데이터를 찾을 떄 이진검색은 전체 배열의 중간값에서부터 찾는다.
중간값인 10을 기준으로 13이 큰가 작은가? => 크다. 그러면 10보다 작은 상자는 볼 필요가 없다.
다음, 11~20 의 중간값인 15보다 13이 큰가 작은가? => 작다. 그러면 15보다 큰 상자는 볼 필요가 없다.
...
이와 같이 1/2 => 1/2 => .. 의 형식으로 가기 때문에 선형검색으로는 20스텝이 필요할 내용을 이진검색은 4번의 스텝으로 값을 찾을 수 있게 된다.
3. BigO
3-1 상수시간 (Constant time)
public class BigO {
public static void main(String[] args){
int i = 10; // ... i의 갯수가 몇개가 되듯
int[] arr = new int[i];
arr[0] = 2;
// BigO = O(1)
System.out.println(arr[0]);
// BigO = O(1)
System.out.println(arr[0]);
System.out.println(arr[0]);
}
}
arr[i]의 개수, 즉 배열로 할당되는 상자의 갯수가 3개, 5개, 10개, 100개가 되든 println(arr[0])으로 출력되는 과정은 단 한번, 하나의 스텝으로 출력이 된다.
이렇게 정해진 상수를 출력하는 것을 상수시간 알고리즘 (Constant time algorithm)이라고 한다.
또한 이러한 println을 두번, 세번, 네번 반복하여, 전체 함수를 종료하기까지의 스텝이 2번, 3번, 4번으로 증가한다 할지라도 BigO 적인 표현으로 O(2) 로 변화하지는 않는다. 여전히 이것은 O(1) 이다.
3-2 선형 시간복잡도
public class BigO2 {
public static void main(String[] args) throws IOException {
int[] arr = new int[] {1, 3, 5, 2, 4};
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
이 코드 상의 arr 배열의 공간은 5개이고, 따라서 5번 호출한다.
만약 배열이 100개라면 100번 호출할 것이다. 배열이 커질수록 필요 스텝도 커질 것이다.
이는 BigO적으로 표현한다면 O(N) 이 된다. 즉 선형검색과 BigO적인 표현은 똑같아진다.
3-3 2차 시간복잡도(Quadratic time) => Nested Loops 가 있을 때 발생
public class BigO3 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N - i; j++) {
System.out.print(" ");
}
for (int k = 1; k <= i; k++) {
System.out.print("*");
}
System.out.println(); }}}
위와 같은 for문(loop문) 안에 for문이 들어있는 경우, 시간복잡도는 input N값의 ^2 이상이 된다.
3-4 로그 시간복잡도 (Logarithmic time) => Binary Search 에서 발생한다.



BigO에서 log'2'32 '2'라는 것은 배제하고 표시한다.
따라서 선형 시간복잡도보다는 빠르고, 상수시간복잡도보다는 느리다.
또한 로그시간복잡도는 이진검색이라는 특성 상 정렬 과정의 스텝이 추가된다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] 안정 정렬과 불안정 정렬 (0) | 2022.02.22 |
|---|---|
| [Algorithm] Recursion(순환) 의 개념, 파보나치 수, 최대공약수 (0) | 2022.02.16 |
| [Algorithm] chapter01-1 시간복잡도 (0) | 2022.02.11 |











